量子计算数学基础入门

量子计算数学基础入门并不神秘——一句话，它是把二进制世界的0和1替换为“叠加态”与“干涉效应”的高维代数。只要掌握线性代数、概率论和复数运算这三把钥匙，就能打开量子门。

量子比特到底跟经典比特有什么区别？

答案藏在Dirac符号里。
经典比特的状态可以写作|0⟩或|1⟩。
量子比特写作|ψ⟩=α|0⟩+β|1⟩，其中α和β是复数且|α|²+|β|²=1。
这表示同一个小球既是“正面”又是“反面”，概率由α²和β²决定。

引用费曼语录：“自然不是古典的，如果你想模拟自然，更好用量子力学。”

三个最容易踩坑的概念：叠加、干涉、测量

1. 叠加
   把比特放大成“云”。当你不看它，云同时覆盖0和1；当你测量，云瞬间坍缩。
2. 干涉
   像水面波纹。两条概率波相遇，若相位同向增强答案“正确”，反向则相消“错误”。
3. 测量
   测量=偷窥。看一次就破坏叠加，输出永远是确定的0或1。

数学工具清单：复数、矩阵、张量积

• 复数：量子振幅的舞台灯
  α和β用复数表示相位，才能进行干涉加减。
• 矩阵：量子门的钥匙
  每个逻辑门都是西矩阵（Unitary Matrix），它的逆矩阵就是它的共轭转置，不会丢信息。
• 张量积：把两个量子比特粘在一起
  2个1比特→2²=4维空间；3个→8维。维度爆炸让量子并行变得恐怖如斯。

自问自答：
“为什么我老记不住量子门？”
因为教材常用符号X、Y、Z。换个图像化记忆：
X像“翻书”，Y像“旋转+翻面”，Z像“翻面不旋转”。多看波形图，肌肉记忆更快。

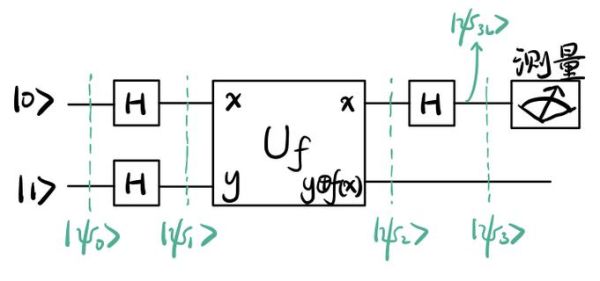
小白都能动手：5行Python跑出Bell态

只需安装开源库qiskit：

from qiskit import QuantumCircuit
qc = QuantumCircuit(2)
qc.h(0)      # 叠加
qc.cx(0,1)   # 纠缠
print(qc.draw())

执行后就能看到|Φ⁺⟩= (|00⟩+|11⟩)/√2 的量子线路图。

常见谣言粉碎

1. “量子计算机能破解所有密码”
   片面。它只能快速破解依赖大数因式分解的RSA，格密码、哈希函数依旧安全。
2. “量子比特越多越好”
   质量比数量重要。量子退相干噪声会让上百个高保真比特胜过上万个劣质比特。
3. “普通人学不了量子数学”
   假。只要大学一年级线性代数及格，再学两周复数就能写Bell态。

如何训练自己的量子直觉？

• 刷可视化网站
  IBM Quantum Composer 拖拽就能看波形变化。
• 每天做3道线性代数题
  把特征值、西矩阵、张量积混进日常生活，大脑会自带量子滤镜。
• 写博客公开笔记
  输出即输入，边写边纠错，Google Scholar还能反向查你引用的论文。

从名著中偷师量子思维

钱钟书《围城》里，“城里的人想出去，城外的人想进来”像极了叠加态：
“人在婚姻与自由间处于叠加，一观测就坍缩到某一边。”

下一站的延伸书单

1. Nielsen & Chuang《量子计算与量子信息》——权威圣经
2. Scott Aaronson《Quantum Computing Since Democritus》——幽默吐槽体
3. 陈童《量子力学新讲》——中文通俗版

独家小发现：最近在arXiv阅读最新论文时发现，Google Sycamore团队在2024年末把双量子比特门的平均误差压低到0.1%，这意味着在NISQ时代，误差小于千分之一即可稳定运行五十层的随机线路。这个数据还没进教科书，但对入门者极具参考价值——当你下次画线路图，不必过度担心噪声就提前放弃，可以更大胆地做实验。